heterophily

heterophily与heterogeneity不同。Heterogeneity更多地与推荐系统中的节点类型差异有关，例如用户和项目节点，但heterophily是具有相同类型的节点下的邻居之间的特征或标签差异。传统的GNN通常假设相似的节点（特征/类）连接在一起，但“对立吸引”现象也广泛存在于一般图中。

这个github仓库收集了跟heterophily有关的论文：https://github.com/alexfanjn/Graph-Neural-Networks-With-Heterophily

ICLR2023中了的heterophily的相关论文

Gradient Gating for Deep Multi-Rate Learning on Graphs

粒子动力学观点：ACMP: Allen-Cahn Message Passing with Attractive and Repulsive Forces for Graph Neural Networks, ICLR OpenReview

提供新的benchmark数据集：A critical look at the evaluation of GNNs under heterophily: Are we really making progress?

动态图？：GReTo: Remedying dynamic graph topology-task discordance via target homophily

AAAI2022合集：https://ojs.aaai.org/index.php/AAAI/issue/archive

AAAI2022中heterophily的相关论文

Block Modeling-Guided Graph Convolutional Neural Networks，code

Powerful Graph Convolutioal Networks with Adaptive Propagation Mechanism for Homophily and Heterophily，code

Deformable Graph Convolutional Networks

Graph Pointer Neural Networks

首先是2022的一篇综述：Graph Neural Networks for Graphs with Heterophily: A Survey

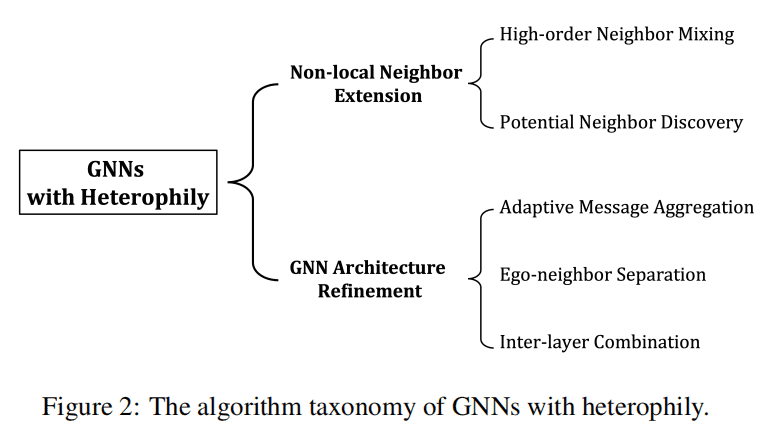
作者在文中使用的分类方法

这个分类对应解决了两个问题：（1）如何发现合适的邻居；（2）如何利用所发现的邻居的信息。

Non-local Neighbor Extension

local neighborhood 的定义在heterophilic图上是不恰当的，因为同一类的节点表现出很高的结构相似性，但彼此之间可能更远。两种方法可以从遥远但信息丰富的节点中捕获重要的特征，进而改进heterophilic GNNs的能力。

High-order neighbor mixing

从节点的本地一跳邻居和k-hop跳邻居那里接收潜在的表示。代表性工作：

  1. MixHop：除了one-hop邻居外，还考虑了two-hop neighbors来进行消息传播。然后，从不同跳获得的消息通过不同的线性变换进行编码然后mixed by concatenation
  2. H2GCN：在每个消息传递步骤中聚合来自higher-order neighbors的信息。验证了当中心节点的one-hop邻居的标签有条件地独立于该节点的标签时，其two-hop邻居倾向于包含更多的与中心节点同一类的节点。

Potential neighbor discovery

重新考虑异质图中的邻居定义，通过异质性下的整个拓扑探索构建新的structural neighbors。其中，s(v, u) 度量在特定定义的潜在空间中，节点u和v之间的距离。τ是控制邻居数量的阈值。

\[ N_{p}(v)={u:s(v,u)<τ} \]

  1. Geom-GCN：符合文中所定义的几何关系的节点，也参与了GCN的消息聚合。

GNN Architecture Refinement

一般的GNN结构包含两部分： \[ \begin{split} \begin{aligned} m_{v}^{(l)} &=AGGREGATE^{(L)} ({h_{u}^{(l-1)}:u\in N(v)}),\\ h_{v}^{(l)} &=UPDATE^{(L)}({h_{v}^{(l-1)},m}_{v}^{(l)}) \end{aligned} \end{split} \] 聚合函数整合已发现的邻居的信息，更新函数将学习到的邻居消息与初始的ego representation结合起来。

针对异质图上的原始局部邻居和扩展的非局部邻居，现有的GNN体系结构细化方法通过相应地修改聚合和更新函数来充分利用邻居信息。

Adaptive Message Aggregation

在异质图上整合有益信息的关键是区分相似邻居（可能在同一类中）的信息和不相似的邻居（可能属于不同的类别）的信息。

方法：在聚合操作中，对第l层的节点对(u, v)施加 adaptive edge-aware 的权值\(a_{u,v}^{(l)}\)来改变聚合操作 \[ m_{v}^{(l)}=AGGREGATE^{(L)} (a_{u,v}^{(l)}{h_{u}^{(l-1)}:u\in N(v)}),\\ \] 文中分别提供了现有方法在谱域和空间域采用的权值分配方案。其中，spectral GNNs使用图信号处理的理论来设计图的滤波器，而spatial GNNs则利用图的结构拓扑来开发聚合策略。

spectral domain

与同质图上近似计算图傅里叶变换 (graph Fourier transformation) 的拉普拉斯平滑 (Laplacian smoothing)和低通滤波 (low-pass fifiltering)相比，异质图上的spectral GNNs包括低通和高通滤波器，以自适应地提取低频和高频图信号。其背后的本质直觉在于，低通滤波器主要保留了节点特征的共性(commonality)，而高通滤波器则捕获了节点之间的差异。

 FAGCN采用self-gating注意力机制，通过将\(a_{u,v}^{(l)}\)分成两个分量，i.e.,\(a_{u,v}^{(l,LP)}\) and \(a_{u,v}^{(l,HP)}\)，来学习低频信号和高频信号的比例。通过自适应频率信号学习，FAGCN可以在不同类型的图上实现具有同质性和异质性的表达性能。

spatial domain

在spatial domain中，异质性gnn需要来自相同或不同类别的邻居的基于拓扑的不同聚合，而不是同质性gnn的average aggregation。因此，应根据空间图的拓扑结构和节点标签来分配邻居的边感知权值(edge-aware weights)。

DMP以节点属性为弱标签，并考虑不同消息传递的节点属性异质性，并每条边指定每个属性传播权重。

Ego-neighbor separation

在异质图上，一个ego node的类标签很可能与其相邻的节点不同。因此，将ego node representation与邻居节点的聚合表示分开encode将有利于可区分的node embedding learning。

ego-neighbor separation method在聚合过程中分开中心节点的自循环连接，同时把更新过程改为non-mixing operations，例如concatenation，而不是混合操作，例如vanilla GCN中的average。

H2GCN首先提出去掉自循环连接(self-loop connection)，并且指出，更新函数中的非混合操作确保了表达性节点的表示能在多轮传播中存活下来，而不会变得非常相似。 WRGNN对ego-node embedding及其邻居聚合消息使用不同的映射函数。

Inter-layer combination

前面的两种方法深入研究了GNN的每一层，而Inter-layer combination考虑了层间操作来提高异质性下GNN的表示能力。

这个方法的直觉是，GNN的浅层(shallow layers)收集局部信息，e.g.两层vanilla GCN中的一跳邻居位置，随着层的深入，GNN通过多轮邻居传播逐渐隐式地捕获全局信息。

在异质性设置下，具有相似信息的邻居，即类标签，可能同时在局部几何(local geometry)和长期全局拓扑中(long-term global topology)定位。因此，结合来自每一层的中间表示有助于利用不同的邻域范围，并同时考虑局部和全局结构属性，从而产生强大的异质性GNNs。

这一想法最早来自于 JKNet，它首先在同质图上灵活地捕获不同邻域范围下更好的structure-aware representation。由于异质图上的结构拓扑更加复杂。 H2GCN将之前所有层的节点表示连接起来，并在最后一层清晰地学习异质性节点特征。

ICLR2023上的相关论文

Beyond Smoothing: Unsupervised Graph Representation Learning with Edge Heterophily Discriminating

Motivation

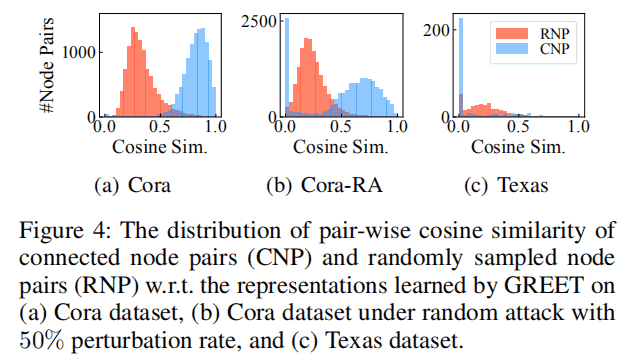
已有的方法平滑相邻节点的表示，同时，为给表示学习提供监督信号，他们经常使用保持局部平滑性的目标，即鼓励在同一边内的节点表示、随机游走或子图具有更高的相似性。因此，所有的节点都被迫具有与它们的邻居相似的表示。如下图，所有连接的节点在表示空间中都被推得更近，即使其中一些节点与随机采样的节点相比只是具有适度的特征相似性。

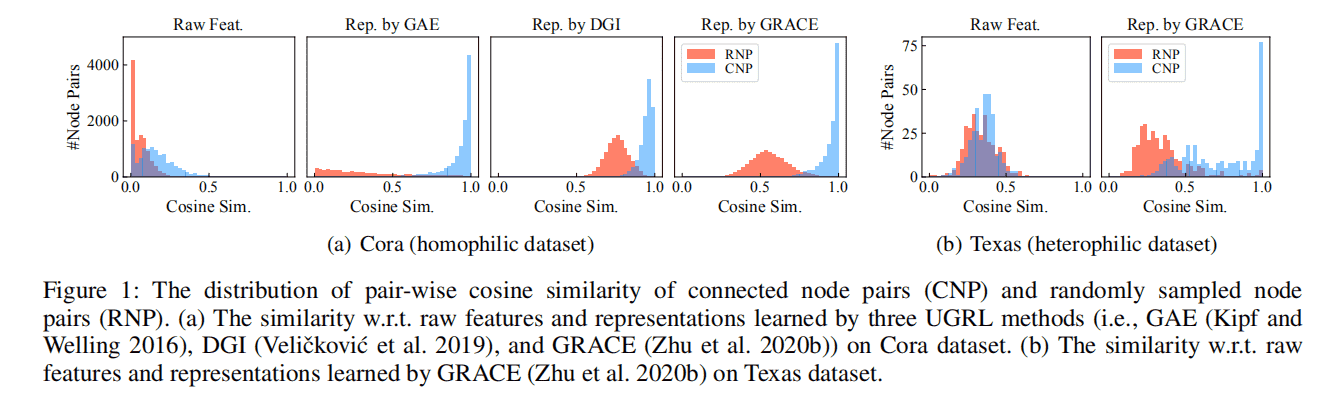
(Q1) Is it possible to distinguish between two types of edges in an unsupervised manner ?

在无监督的场景下，很难仅通过节点特征和图结构来区分边缘类型，特别是大量的边连接的是具有中等相似性的节点对。

(Q2) How to effectively couple edge discriminating with representation learning into an integrated UGRL model?

作者想要找到一个良好的相互作用方案，使边识别和表示学习相互促进。

Methodology

Edge Discriminating

用vectorial structural encoding(a.k.a. positional encoding)对结构特征进行建模，通过将节点结构编码（位置编码）与原始特征连接起来，可以保留有效的证据。（本文使用的结构编码是Dwivedi et al. 2022的基于随机游动扩散过程）

节点\(v_{i}\)的\(d_{s}\)维结构编码\(s_{i}\)可以通过基于\(d_{s}\)-step随机游走的graph diffusion来计算

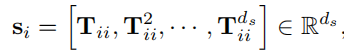
其中\(T = AD^{-1}\)是随机游走的转移矩阵。

图增广方法有特征增广、结构增广、混合增广。

特征增广主要对图数据中的特征信息进行变换，最常见的手段是节点特征遮盖（NFM），即随机的将图中的一些特征量置为 0；此外，节点特征乱序（NFS）也是一种特征增广方法，其手段为对调不同节点的特征向量。

结构增广的手段是对图结构信息进行变换，常见的结构增广为边修改（EM），包括对边的增加和删除；另一种结构增广为图弥散（Graph diffusion，GD），其对不同阶的邻接矩阵进行加权求和，从而获取更全局的结构信息。

混合增广则结合了上述两种增广形式，一个典型的手段为子图采样（SS），即从原图数据中采样子结构成为增广样本。

——对graph diffusion的一个扩展

以原始特征和结构编码为输入，边鉴别器用两个MLP层估计homophily的概率：

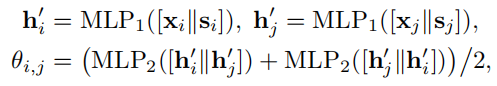
[·||·]表示连接操作，\(h_{i}^{'}\)是节点\(v_{i}\)的中间嵌入，\(\theta_{i,j}\)是\(e_{i,j}\)的估计的homophily概率。为了使估计不受边方向的影响，我们将第二层MLP层应用于不同顺序的嵌入连接(embedding concatenations)。

利用估计的概率\(\theta_{i,j}\)，作者想从伯努利分布\(w_{i,j}\sim Bernoulli(\theta_{i,j})\)中采样一个二分类的homophily指标\(w_{i,j}\)，\(w_{i,j}=0\)代表homophily，\(w_{i,j}=1\)代表heterophily。然而，这种采样是不可微的，会使得鉴别器难以训练。为解决这个问题，作者采用Gumbel-Max重参数化技巧来近似二进制指标\(w_{i,j}\)。具体地说，离散的同质性指标\(w_{i,j}\) is relaxed to一个连续的homophily weight \(\hat{w}_{i,j}\)：

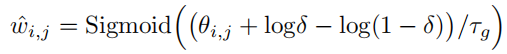
其中，\(\delta \sim Uniform(0,1)\)为抽样的Gumbel随机变量，\(\tau_{g}>0\)为 temperature hyper-parameter。当\(\tau_{g}\)接近0时，\(\hat{w}_{i,j}\) tends to be sharper（更接近0或1）。

为了使边鉴别可训练，作者没有明确地将边分为同质和异质两类，而是在后面homophilic/heterophilic这两个view上work的时候，为每个边分配一个软权重。

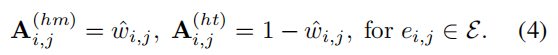
ranking loss：学习多个输入之间的关系。这种任务也叫metric learning，即通过学习将原始输入投影到一个新的空间中，在这个空间里相似输入将表现出距离相近，而不同输入将表现出距离甚远。

Dual-Channel Encoding

为了从homophilic和heterophilic view中学习信息表示，作者设计了两个不同的编码器，它们分别在两个不同的vi上执行低通和高通graph filtering。根据homophily边获取相似节点之间共享的信息，根据heterophily边从dissimilar的邻居中过滤出不相关的信息。

  1. 具体地说，在homophilic view中，相似节点彼此连接，我们用低通图滤波器沿着homophilic结构平滑节点特征。低通滤波可以捕获图信号中的低频信息，从而保持相似节点的共享知识。GREET种使用的是一个简单的低通GNN，即SGC。
  2. 与homophilic view不同，heterophilic view包含连接不同节点的边，使用高通图滤波，沿边锐化节点特征并保留高频图信号。从而区分不同但连接的节点的表示。从图信号处理的角度来看，图拉普拉斯算子（即与图拉普拉斯矩阵L相乘）已被证明可以有效地捕获高频分量。因此使用Lap-SGC，来对heterophilic view进行高通滤波。

使用两个不同的编码器（即SGC和Lap-SGC）获得两组分别捕获低频和高频信息的表示。最终节点表示通过连接由两个视图的表示得到。

Model Training

使用Pivot-Anchored Ranking Loss训练边判别，使用contrastive loss训练representation encoders，还引入了一种交替训练策略来迭代优化两个组件。

  1. Pivot-Anchored Ranking Loss：边识别的目标是区分homophilic（连接相似节点）和heterophilic（连接不同节点）边，其主要的挑战是找到“相似”和“不同”之间的界限。作者建议使用随机抽样的节点对作为相似度度量的“轴”(Pivot)，以确保由homophilic连接的节点对明显比“轴节点对”更相似，而由heterophilic连接的节点明显比“轴节点对”更不同。
  2. Robust Dual-Channel Contrastive Loss
  3. Training Strategy ：边识别模块的训练依赖于节点的表示来度量节点的相似性；表示学习反过来从边识别提供的视图生成表示。为了有效地训练两个组件，随着这两个组件的相互增强，作者采用交替训练策略来交替优化边识别和节点表示学习。总体优化目标可以写为\(L=L_{r}+L_{c}\)。为了提高表示模块的泛化能力，作者采用数据增强来增加模型训练的数据多样性：feature masking和edge dropping，以扰乱两个视图的特征和结构。

Experiment

  1. 作者也用adversarial attack进行攻击，证明模型的鲁棒性
  2. 首尾呼应，依旧可视化了Cora、扰动后的Cora和Texas的 pair-wise representation similarity
    • 在(a)中，对于Cora数据集中的大多数边缘，末端节点的表示是相似的；值得注意的是，对于一小部分被识别为heterophilic的边，它们的相似性更接近于0。证明GREET可以分离 homophilic and heterophilic edges，并产生可区分的表示。
    • (b)：在受扰动的Cora中，大量的边被检测为heterophilic，两端节点表示是不同的。由于GREET具有识别噪声边缘的能力，因此在对抗攻击面前显示出了很强的鲁棒性
    • (c)中也可以发现了类似的现象，其中大部分边被识别为heterophilic。分离的两种类型的边带来了更多的信息表示，从而导致了GREET在heterophilic图上的优越性能。