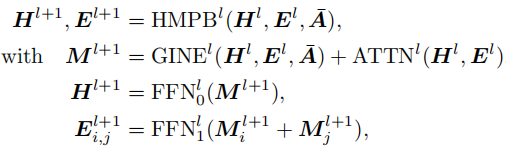综述-Generative Diffusion Models on Graphs: Methods and Applications

主要应用在molecule and protein modeling
现有方法分为两类：
- 自回归生成（autoregressive generation）：按照决策序列的顺序一步一步地生成期望的图（具有拓扑结构和整个图节点/边缘特征）。
  - 单样本生成（one-shot generation）：在一个步骤中生成具有拓扑结构和节点/边特征的完整的图
分子图生成面临的挑战：
- Discreteness（离散性）：图结构是离散的，导致模型的梯度计算困难。因此不能将广泛使用的优化算法直接以端到端的方式引入到图生成的反向传播训练中。
- Complex Intrinsic Dependencies（复杂的内在依赖）：与图像数据不同，节点不是独立同分布（i.i.d.）的，这种图结构的复杂性为生成所需的图带来了巨大的挑战。
- Permutation Invariant（置换不变性）：由于节点在大多数图中自然是无序的，所以最多有N!个不同的等效邻接矩阵代表具有N个节点的相同图。

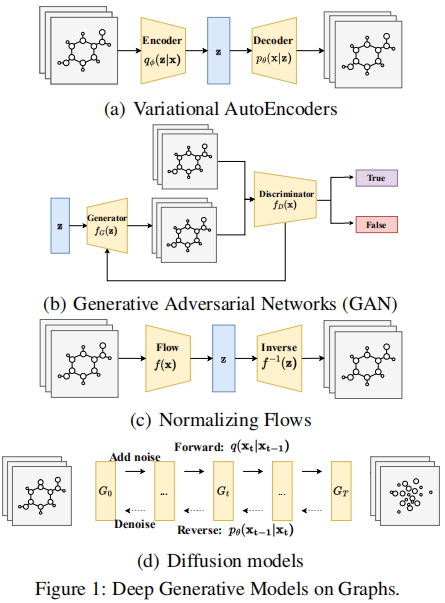
GraphVAE构造两个GNN作为encoder和decoder来估计图的分布，但由于基于似然的方法，VAE难以通过后验估计来生成真实的大规模图，并且需要昂贵的计算来实现排列不变性。
基于GAN的方法更容易出现图结构数据的模式崩溃，并且需要额外的计算来训练discriminator。由于图的离散性，大多数基于GAN的方法都通过强化学习技术进行优化
归一化流利用一系列可逆函数f (x)来映射图样本，但由于特殊架构的约束，基于流的生成模型（flow-based generative models）很难完全学习图形的结构信息。
受非平衡热力学理论的启发，扩散生成范式可以被建模为用变分推理训练的马尔可夫链

Diffusion Models

扩散模型的三种范式：SMLD和DDPM分别利用分数匹配思想和非平衡热力学来学习扩散过程的不同反向函数。SGM推广了离散扩散的计算方法并进一步利用随机微分方程（SDE）对扩散过程进行建模。

Score Matching with Langevin Dynamics (SMLD) score matching是什么意思
1. 逐步向数据分布添加随机噪声直到预定义的先验（通常是高斯噪声），然后通过学习数据分布的梯度\(\nabla_{\mathbf{x}} \log p(\mathbf{x})\)来逆转扩散过程，SMLD用一系列可以建模的增量噪声\(q_{\sigma}(\tilde{\mathbf{x}} \mid \mathbf{x}):=\mathcal{N}\left(\tilde{\mathbf{x}} \mid \mathbf{x}, \sigma^{2} I\right)\)来扰动原始分布
Denoising Diffusion Probabilistic Model (DDPM)
Score-based Generative Model (SGM)
1. w

Future Challenges and Opportunities

Discrete Nature of Graphs：现有的图像扩散模型都是在连续空间中开发的。相比之下，图结构数据的离散特性使得很难直接部署扩散模型。一些工作试图通过引入离散概率分布或弥合连续和连续数据之间的差距，使扩散模型适合用于离散数据离散空间，但仍然缺乏一种普遍的和公认的方法来解决这个问题。
Conditional Generation for Graph Diffusion Models：将条件纳入生成模型对于指导所需的生成至关重要，而不是生成新的随机样本，生成具有特定性质的分子和蛋白质具有重要的意义。因此，将额外的信息作为条件引入图扩散模型已成为一个必要的研究方向。一种类型的额外知识可以通过知识图谱形成。在特定领域使用知识图可以帮助控制生成过程以获得所需的图，并增强graph生成的多样性。除了知识图外，还可以考虑其他辅助知识（如视觉知识和文本知识）来推进图扩散模型的设计。
Trustworthiness for Graph Diffusion Models：近年来，人们对人工智能模型可信度的关注日益增加。作为最具代表性的人工智能应用程序之一，graph生成可能会对不同现实任务的用户造成意外伤害，特别是在药物发现等安全关键领域的任务。例如，数据驱动的graph图扩散模型是脆弱的，很容易受到来自恶意攻击者的对抗性攻击；由于图扩散架构的复杂性，理解和解释图生成的工作机制是非常具有挑战性的。在实现可信的图生成方面有几个关键的维度，如安全性和鲁棒性、可解释性、公平性和隐私。因此，如何建立可信的图扩散模型已成为学术界和工业界的关键。
Evaluation Metrics：对图生成的评估仍然是一个挑战。大多数现有的度量标准通常是基于图的统计量和属性（例如，节点的度和稀疏性），这不是完全可靠的。同时，图生成的有效性和多样性在不同的应用中也很重要。因此，需要努力定量地测量生成的图的质量。

未来前景

Recommender Systems：图上的扩散模型有可能对给定用户的项目进行条件分布建模，以便更好地为用户生成推荐列表。
Graph Anomaly Detection：扩散模型可以用来净化图像数据，以获得更好的对抗性鲁棒性。因此，图的扩散模型为改进图的异常检测提供了巨大的机会，从而使增强了图模型对对抗性攻击的鲁棒性。
Causal Graph Generation：因果推理是指旨在建立因果关系之间联系的统计数据，通常由因果关系图形成。实际上，分析了因干扰而引起的因果关系是很困难的。例如，临床试验不是简单地使用控制变量，而是使用因果推理来评估该治疗方法的有效性。在因果发现任务中，可以生成因果-效应图，以帮助分析因果关系之间的联系，从而提高下游任务的准确性和获得可解释性。因此，图扩散模型提供了增强因果效应图生成的机会，这有助于减少可能的偏差，建立健壮的模型，并带来解释模型如何工作的新见解。

Conditional Diffusion Based on Discrete Graph Structures for Molecular Graph Generation

Motivation

学习分子图的潜在分布和生成高保真样本是药物发现和材料科学中的一个基础研究问题。然而，准确地建模分布和快速生成新的分子图仍然是关键和具有挑战性的目标。

现有的主要问题是分子图的质量和采样速度，作者认为，其背后有两个原因：

专注于实数图的表述(将分子表示为节点特征和边特征矩阵)，而忽略了离散的图结构，使得难以从有噪声的实数矩阵中提取准确的局部基元进行去噪并保持接近真实的图分布
一个简单的图神经网络设计可能不足以完全从损坏的图中建模节点边依赖关系，并进一步满足复杂的生成需求

考虑图的离散性和设计合适的图噪声预测模型

Methodology

Conditional Graph Diffusion

首先定义一个正向过程，该过程用噪声序列扰动数据，直到输出分布成为已知的先验分布。

将graph构造为由节点特征矩阵和边类型矩阵组成的高维变量即可应用扩散模型 \(G \in R^{N\times F} \times R^{N\times N}\)，作者认为，那些被忽略的离散图结构（例如星和环）可能为节点边依赖建模和图去噪提供额外的线索。因此提出，将边存在矩阵（邻接矩阵）和边类型矩阵分离，并且使用one-bit的离散变量来表示该边是否存在，从而形成了\(\bar{A} \in \left \{0,1\right \}^{N\times N}\)，进而在每个time step，\(t \in[0,T]\)量化离散图结构\(\bar{A}_t\)。离散图结构可以插入反向过程，并作为条件作用。

score function是求最大对数似然函数中让对数似然函数梯度等于0的梯度

Graph Noise Prediction Model

由于\(\epsilon_\theta(G_t,\bar{A}_t,t)\)能够预测添加到原始图像的噪声，作者将其看作图噪声预测模型。由于实时的实数图状态和图分布学习的复杂要求，直接应用图神经网络是不合适的。并且就分子图而言，这一模型应该关注化学价规则的局部节点边依赖关系并且尝试恢复全局图模式（例如边稀疏性、频繁的环子图，甚至是原子型分布）。

为满足上述挑战，作者提出的混合消息传递模块（hybrid message passing block，HMPB）包含两个不同种类的消息传递层来显式地建模实数矩阵（\(X_t\)和\(A_t\)）和离散矩阵（\(\bar{A}_t\)）中的结构和特征依赖。一种是标准的消息传递层（例如GINE），依赖于解码的离散图结构来聚合局部邻居节点边特征；另一种是一个全连接的基于注意力的消息传递层，专注于全局信息的提取和传递。将第1个HMPB中的节点和边表示更新过程表示为：